티스토리 뷰
자료구조(Data Structure) 배열 (Array) 기본 정리
꿈을 위해 잠을 잊은 그대에게 2020. 5. 17. 19:47배열 (Array)
- C++에서 사이즈 구하기
int arr[] = { 1, 2, 3, 4, 5, 6, 7 };
int n = sizeof(arr) / sizeof(arr[0]); // 7
1. 배열 회전 프로그램

기본적인 회전 알고리즘 구현
#include
using namespace std;
//왼쪽으로 한번 회전
void leftRotatebyOne(int arr[], int n){
int temp = arr[0], i;
for(i = 0; i < n-1; i++){
arr[i] = arr[i+1];
}
arr[i] = temp;
}
// d만큼 회전
void leftRotate(int arr[], int d, int n){
for(int i = 0; i < d; i++)
leftRotatebyOne(arr, n);
}
void printArray(int arr[], int n){
for(int i = 0; i < n; i++)
cout << arr[i] << " ";
}
int main(){
int arr[] = { 1, 2, 3, 4, 5, 6, 7 };
int n = sizeof(arr) / sizeof(arr[0]);
leftRotate(arr, 2, n);
printArray(arr, n);
return 0;
}
temp를 활용해서 첫번째 인덱스 값을 저장 후 arr[0]~arr[n-1]을 각각 arr[1]~arr[n]의 값을 주고, arr[n]에 temp를 넣어준다.
void leftRotatebyOne(int arr[], int n){
int temp = arr[0], i;
for(i = 0; i < n-1; i++){
arr[i] = arr[i+1];
}
arr[i] = temp;
}이 함수를 활용해 원하는 회전 수 만큼 for문을 돌려 구현이 가능
저글링 알고리즘 구현
#include
using namespace std;
// 최대공약수 gcd 활용
int gcd(int a, int b)
{
if (b == 0)
return a;
else
return gcd(b, a % b);
}
void leftRotate(int arr[], int d, int n)
{
for (int i = 0; i < gcd(d, n); i++) {
int temp = arr[i];
int j = i;
while (1) {
int k = j + d;
if (k >= n)
k = k - n;
if (k == i)
break;
arr[j] = arr[k];
j = k;
}
arr[j] = temp;
}
}
void printArray(int arr[], int size)
{
for (int i = 0; i < size; i++)
cout << arr[i] << " ";
}
int main()
{
int arr[] = { 1, 2, 3, 4, 5, 6, 7 };
int n = sizeof(arr) / sizeof(arr[0]);
// Function calling
leftRotate(arr, 2, n);
printArray(arr, n);
return 0;
} 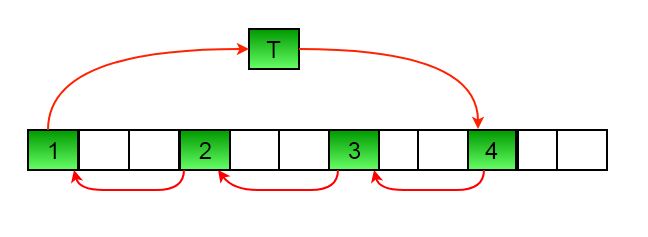
최대공약수 gcd를 이용해 집합을 나누어 여러 요소를 한꺼번에 이동시키는 것
위 그림처럼 배열이 아래와 같다면
arr[] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}
1,2,3을 뒤로 옮길 때, 인덱스를 3개씩 묶고 회전시키는 방법이다.
a) arr [] -> { 4 2 3 7 5 6 10 8 9 1 11 12}
b) arr [] -> {4 5 3 7 8 6 10 11 9 1 2 12}
c) arr [] -> {4 5 6 7 8 9 10 11 12 1 2 3 }
역전 알고리즘 구현
#include <iostream>
using namespace std;
// swap을 활용한 reverse 구현
void reverseArr(int arr[], int start, int end){
while (start < end){
int temp = arr[start];
arr[start] = arr[end];
arr[end] = temp;
start++;
end--;
}
}
// d로 나눠서 역전 알고리즘 수행
void rotateLeft(int arr[], int d, int n){
reverseArr(arr, 0, d-1);
reverseArr(arr, d, n-1);
reverseArr(arr, 0, n-1);
}
void printArray(int arr[], int n){
for(int i = 0; i < n; i++){
cout << arr[i] << " ";
}
}
int main(void){
int arr[10] = {1,2,3,4,5,6,7,8,9,10};
int n = sizeof(arr) / sizeof(arr[0]);
int d = 3;
rotateLeft(arr, d, n);
printArray(arr, n);
return 0;
}회전시키는 수에 대해 구간을 나누어 reverse로 구현하는 방법
d = 2이면
1,2 / 3,4,5,6,7로 구간을 나눈다.
첫번째 구간 reverse -> 2,1
두번째 구간 reverse -> 7,6,5,4,3
합치기 -> 2,1,7,6,5,4,3
합친 배열을 reverse -> 3,4,5,6,7,1,2
- swap을 통한 reverse
void reverseArr(int arr[], int start, int end){
while (start < end){
int temp = arr[start];
arr[start] = arr[end];
arr[end] = temp;
start++;
end--;
}
}- 구간을 d로 나누었을 때 역전 알고리즘 구현
void rotateLeft(int arr[], int d, int n){
reverseArr(arr, 0, d-1);
reverseArr(arr, d, n-1);
reverseArr(arr, 0, n-1);
}
2. 배열의 특정 최대 합 구하기
예시) arr[i]가 있을 때, i*arr[i]의 Sum이 가장 클 때 그 값을 출력하기
(회전하면서 최대값을 찾아야한다.)
Input: arr[] = {1, 20, 2, 10}
Output: 72
2번 회전했을 때 아래와 같이 최대값이 나오게 된다.
{2, 10, 1, 20}
20*3 + 1*2 + 10*1 + 2*0 = 72
Input: arr[] = {10, 1, 2, 3, 4, 5, 6, 7, 8, 9};
Output: 330
9번 회전했을 때 아래와 같이 최대값이 나오게 된다.
{1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
0*1 + 1*2 + 2*3 ... 9*10 = 330
접근 방법
arr[i]의 전체 합과 i*arr[i]의 전체 합을 저장할 변수 선언
최종 가장 큰 sum 값을 저장할 변수 선언
배열을 회전시키면서 i*arr[i]의 합의 값을 저장하고, 가장 큰 값을 저장해서 출력하면 된다.
해결법
회전 없이 i*arr[i]의 sum을 저장한 값
R0 = 0*arr[0] + 1*arr[1] +...+ (n-1)*arr[n-1]
1번 회전하고 i*arr[i]의 sum을 저장한 값
R1 = 0*arr[n-1] + 1*arr[0] +...+ (n-1)*arr[n-2]
이 두개를 빼면?
R1 - R0 = arr[0] + arr[1] + ... + arr[n-2] - (n-1)*arr[n-1]
2번 회전하고 i*arr[i]의 sum을 저장한 값
R2 = 0*arr[n-2] + 1*arr[n-1] +...+ (n?1)*arr[n-3]
1번 회전한 값과 빼면?
R2 - R1 = arr[0] + arr[1] + ... + arr[n-3] - (n-1)*arr[n-2] + arr[n-1]
여기서 규칙을 찾을 수 있음.
Rj - Rj-1 = arrSum - n * arr[n-j]
이를 활용해서 몇번 회전했을 때 최대값이 나오는 지 구할 수 있다.// 지정된 배열에서 하나씩 회전을 해서 i*arr[i]의 합이 가장 컸을 때 값을 출력하는 문제
#include <iostream>
using namespace std;
int maxVal(int arr[], int n){
int arrSum = 0; // arr[i]의 전체 합
int curSum = 0; // i*arr[i]의 전체 합
for(int i = 0; i < n; i++){
arrSum = arrSum + arr[i];
curSum = curSum + (i*arr[i]);
}
int maxSum = curSum;
for (int j = 1; j < n; j++){
curSum = curSum + arrSum - n*arr[n-j];
if ( curSum > maxSum )
maxSum = curSum;
}
return maxSum;
}
int main(void){
int arr[] = {1,20,2,10};
int n = sizeof(arr) / sizeof(arr[0]);
cout << maxVal(arr, n);
return 0;
}
3. 특정 배열을 arr[i] = i로 재배열 하기
예시) 주어진 배열에서 arr[i] = i이 가능한 것만 재배열 시키기
Input : arr = {-1, -1, 6, 1, 9, 3, 2, -1, 4, -1}
Output : [-1, 1, 2, 3, 4, -1, 6, -1, -1, 9]
Input : arr = {19, 7, 0, 3, 18, 15, 12, 6, 1, 8,
11, 10, 9, 5, 13, 16, 2, 14, 17, 4}
Output : [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,
11, 12, 13, 14, 15, 16, 17, 18, 19]arr[i] = i가 없으면 -1로 채운다.
접근 방법
arr[i]가 -1이 아니고, arr[i]이 i가 아닐 때가 우선 조건
해당 arr[i] 값을 저장(x)해두고, 이 값이 x일 때 arr[x]를 탐색
arr[x] 값을 저장(y)해두고, arr[x]가 -1이 아니면서 arr[x]가 x가 아닌 동안을 탐색
arr[x]를 x값으로 저장해주고, 기존의 x를 y로 수정
int fix(int A[], int len){
for(int i = 0; i < len; i++) {
if (A[i] != -1 && A[i] != i){ // A[i]가 -1이 아니고, i도 아닐 때
int x = A[i]; // 해당 값을 x에 저장
while(A[x] != -1 && A[x] != x){ // A[x]가 -1이 아니고, x도 아닐 때
int y = A[x]; // 해당 값을 y에 저장
A[x] = x;
x = y;
}
A[x] = x;
if (A[i] != i){
A[i] = -1;
}
}
}
}
해결법
#include <iostream>
using namespace std;
int fix(int A[], int len){
for(int i = 0; i < len; i++) {
if (A[i] != -1 && A[i] != i){ // A[i]가 -1이 아니고, i도 아닐 때
int x = A[i]; // 해당 값을 x에 저장
while(A[x] != -1 && A[x] != x){ // A[x]가 -1이 아니고, x도 아닐 때
int y = A[x]; // 해당 값을 y에 저장
A[x] = x;
x = y;
}
A[x] = x;
if (A[i] != i){
A[i] = -1;
}
}
}
}
void printArray(int A[], int len){
for(int i = 0; i < len; i++){
cout << A[i] << " ";
}
}
int main() {
int A[] = { -1, -1, 6, 1, 9,
3, 2, -1, 4, -1 };
int len = sizeof(A) / sizeof(A[0]);
fix(A, len);
printArray(A, len);
return 0;
}'Computer Science > Data Structure' 카테고리의 다른 글
| 힙(Heap) (0) | 2020.06.20 |
|---|---|
| 스택(Stack) & 큐(Queue) / 후입선출(LIFO) & 선입선출(FIFO) (0) | 2020.06.19 |
| 자료구조(Data Structure) Array vs ArrayList vs LinkedList (0) | 2020.05.19 |
| 자료구조(Data Structure) 연결리스트 (Linked List) 기본 정리 (0) | 2020.05.18 |
- Total
- Today
- Yesterday
